Program Aplikasi Lingkaran Menggunakan Delphi

Program Aplikasi Lingkaran 2 ( Persamaan Lingkaran )

Ningsih Wahyu Ningsih ¹⁾, Wardatul Islamyah ²⁾

1)      wahyuningsihoct10@yahoo.com , 2) Islamyah.wardatul@yahoo.com

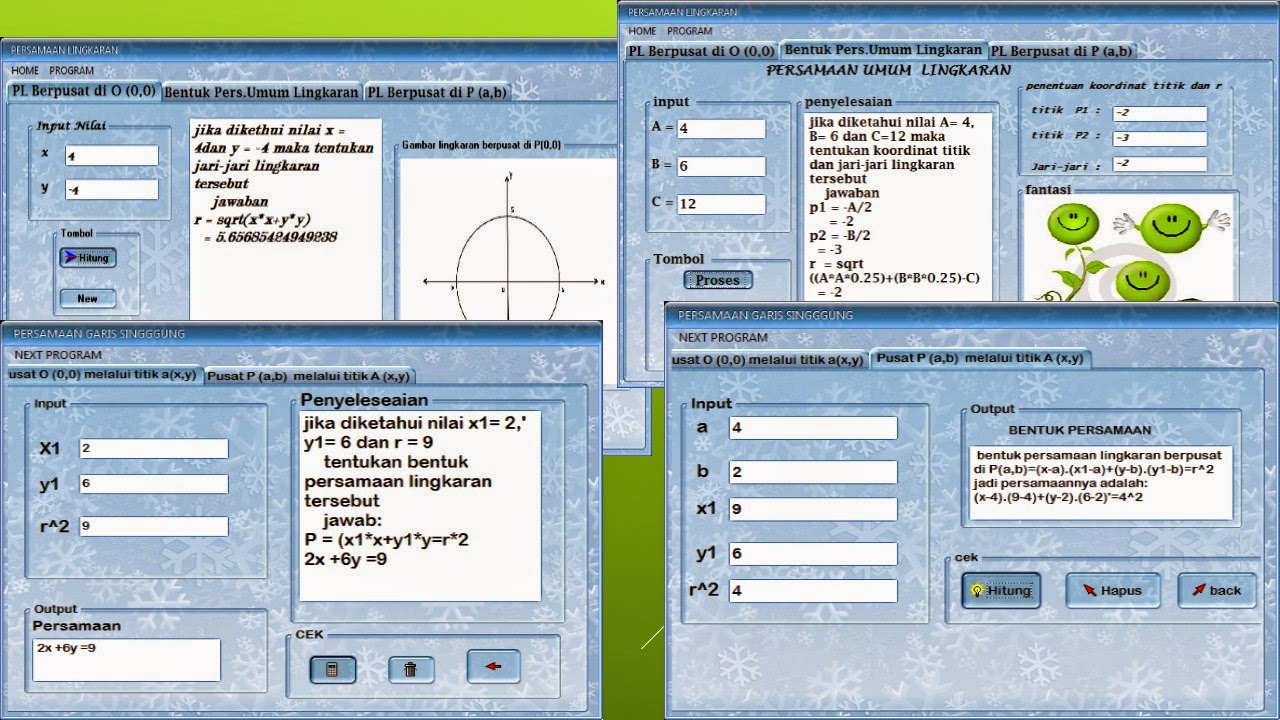
Abstrak – Program aplikasi ini dibuat menggunakan Program Borlan Delphi 7. Program Aplikasi Lingkaran dapat di gunakan dalam mencari persamaan lingkaran. Persamaan lingkaran yang berpusat di P(0,0), P(a,b) serta persamaan umum lingkaran. Dalam program terdapat penghitungan untuk mencari bentuk persamaan garis singgung lingkaran baik yang melewati titik (0,0) dan titik (a,b). selain itu program ini juga menyediakan materi mengecek posisi titik terhadap lingkaran. Program ini terdiri dari 7 form. Adapun isi dari masing-masing form diantaranya: Form pertama adalah form Login, form kedua Program Lingkaran 2 : dimana pada form ini merupakan form yang menampilkan identitas program, form ketiga: Pengenalan Materi, Form keempat : form program persamaan lingkaran. Dalam form keempat ini terdapat 3 New Page yang berisi program persamaan lingkaran yang berpusat di titik (0,0), titik (a,b) dan bentuk persamaan lingkaran. form kelima : form program bentuk persamaan garis singgung lingkaran dan terdapat dua New Page yang berisi program untuk mencari bentuk persamaan garis singgung lingkaran yang berpusat di (0,0) dan (a,b), form keenam : form program mengecek posisi titik terhadap lingkaran dan form ketujuh berisi Identitas Programer.

********

Dalam geometri Euklid, sebuah lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu, yang disebut jari-jari, dari suatu titik tertentu, yang disebut pusat. Lingkaran adalah contoh dari kurva tertutup sederhana, membagi bidang menjadi bagian dalam dan bagian luar.

Download Program Aplikasinya disini.